Contenido
En geometría, un hexágono es un polígono con seis lados. Un hexágono regular tiene seis lados iguales y ángulos iguales. El hexágono regular se reconoce comúnmente en el panal y el interior de la Estrella de David. Un hexaedro es un poliedro de seis lados. Un hexaedro regular tiene seis triángulos con bordes de igual longitud. En otras palabras, es un cubo.
Fórmula del área del hexágono
La fórmula para el área de un hexágono regular con lados de longitud "a" es 3 --- sqrt (3) --- a ^ 2/2, donde "sqrt" indica la raíz cuadrada.
Derivación
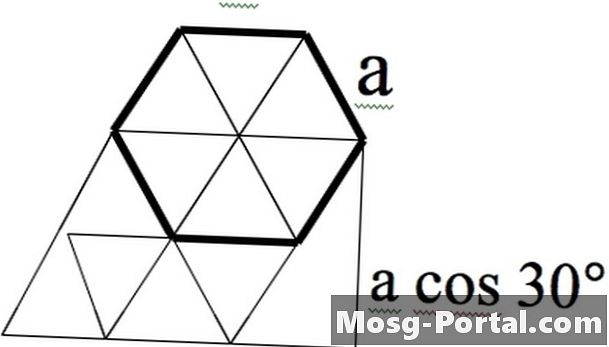
Un hexágono regular puede verse como seis triángulos equiláteros de lados a. Sus ángulos son de 60 grados, por lo que los ángulos en el hexágono son de 120 grados. Los triángulos se pueden extender debajo del hexágono para formar un paralelogramo de lados 2a. Se puede crear un triángulo más grande para determinar la altura de este paralelogramo, que es 2a --- cos 30 ° = a --- sqrt (3).
El paralelogramo en la figura es, por lo tanto, la altura del área --- base = (a --- sqrt (3)) --- 2a = 2 --- sqrt (3) --- a ^ 2.
Pero esto es para un paralelogramo formado por 8 triángulos equiláteros. El hexágono solo estaba compuesto por 6. Por lo tanto, el área de hexágonos es 0.75 de esto, o 3 --- sqrt (3) --- a ^ 2/2.
Derivación Alterna
Los seis triángulos equiláteros en un hexágono tienen lados "a". Sus alturas, h, son, según el teorema de Pitágoras, sqrt = a --- sqrt (3) / 2.
Por lo tanto, el área de un triángulo es (½) --- base --- altura = (a) ---. Seis triángulos en el hexágono dan un área de 3 --- sqrt (3) --- a ^ 2/2.
Fórmula de volumen de hexaedro
La fórmula para el volumen de un hexaedro regular de lados "a" es a ^ 3, ya que un hexaedro regular es un cubo.
El área de superficie es, por supuesto, a ^ 2 --- 6 lados = 6a ^ 2.