
La autocorrelación es un método estadístico utilizado para el análisis de series de tiempo. El propósito es medir la correlación de dos valores en el mismo conjunto de datos en diferentes pasos de tiempo. Aunque los datos de tiempo no se utilizan para la autocorrelación calculada, los incrementos de tiempo deben ser iguales para obtener resultados significativos. El coeficiente de autocorrelación tiene dos propósitos. Puede detectar la no aleatoriedad en un conjunto de datos. Si los valores en el conjunto de datos no son aleatorios, entonces la autocorrelación puede ayudar al analista a elegir un modelo de serie de tiempo apropiado.
Calcule la media o promedio de los datos que está analizando. La media es la suma de todos los valores de datos divididos por el número de valores de datos (n).
Decida un intervalo de tiempo (k) para su cálculo. El valor de retraso es un número entero que indica cuántos pasos de tiempo separan un valor de otro. Por ejemplo, el desfase entre (y1, t1) y (y6, t6) es cinco, porque hay 6 - 1 = 5 pasos de tiempo entre los dos valores. Al probar la aleatoriedad, generalmente solo calculará un coeficiente de autocorrelación usando el retraso k = 1, aunque otros valores de retraso también funcionarán. Cuando esté determinando un modelo de serie de tiempo apropiado, deberá calcular una serie de valores de autocorrelación, utilizando un valor de retraso diferente para cada uno.
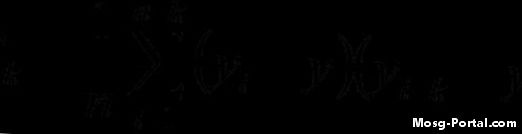
Calcule la función de autocovarianza usando la fórmula dada. Por ejemplo, si estaba calculando la tercera iteración (i = 3) usando un retraso k = 7, entonces el cálculo para esa iteración se vería así: (y3 - y-bar) (y10 - y-bar) Iterar a través de todo valores de "i" y luego tome la suma y divídala por el número de valores en el conjunto de datos.
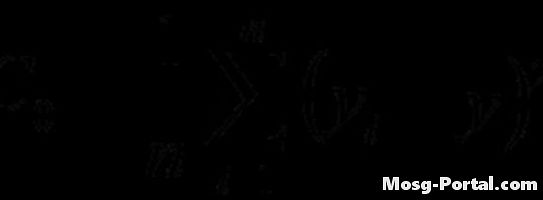
Calcule la función de varianza usando la fórmula dada. El cálculo es similar al de la función de autocovarianza, pero no se usa el retraso.

Divida la función de autocovarianza por la función de varianza para obtener el coeficiente de autocorrelación. Puede omitir este paso dividiendo las fórmulas para las dos funciones como se muestra, pero muchas veces necesitará la autocovarianza y la varianza para otros fines, por lo que también es práctico calcularlas individualmente.