Una elipse se puede definir en geometría plana como el conjunto de puntos de modo que la suma de sus distancias a dos puntos (focos) sea constante. La figura resultante también puede describirse de manera no matemática como un círculo ovalado o "aplanado". Las elipses tienen varias aplicaciones en física y son particularmente útiles para describir las órbitas planetarias. La excentricidad es una de las características de la elipse y es una medida de cuán circular es la elipse.
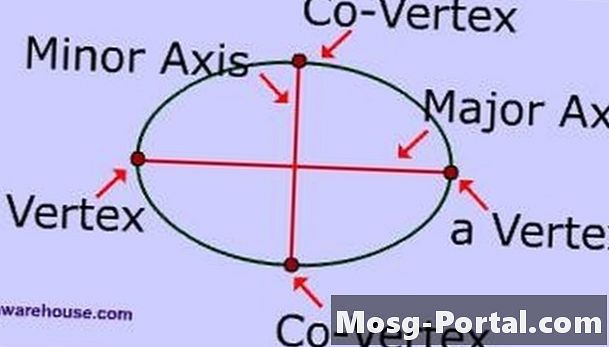
Examina las partes de una elipse. El eje mayor es el segmento de línea más largo que se cruza con el centro de la elipse y tiene sus puntos finales en la elipse. El eje menor es el segmento de línea más corto que se cruza con el centro de la elipse y tiene sus puntos finales en la elipse. El semieje mayor es la mitad del eje mayor y el semieje menor es la mitad del eje menor.
Examina la fórmula para una elipse. Hay muchas formas diferentes de describir matemáticamente una elipse, pero la más útil para calcular su excentricidad es que una elipse es la siguiente: x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1. Las constantes a y b son específicos de una elipse particular y las variables son las coordenadas x e y de los puntos que se encuentran en la elipse. Esta ecuación describe una elipse con su centro en el origen y los ejes mayor y menor que se encuentran en los orígenes x e y.
Identifica las longitudes de los semiejes. En la ecuación x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1, las longitudes de los semiejes están dadas por a y b. El valor más grande representa el semieje mayor y el valor más pequeño representa el semieje menor.
Calcule las posiciones de los focos. Los focos están ubicados en el eje mayor, uno a cada lado del centro. Como los ejes de una elipse se encuentran en las líneas de origen, una coordenada será 0 para ambos focos. La otra coordenada para será (a ^ 2 - b ^ 2) ^ (1/2) para un foco y - (a ^ 2 - b ^ 2) ^ (1/2) para los otros focos donde a> b.
Calcule la excentricidad de la elipse como la relación de la distancia de un foco desde el centro a la longitud del eje semi-mayor. La excentricidad e es por lo tanto (a ^ 2 - b ^ 2) ^ (1/2) / a. Tenga en cuenta que 0 <= e <1 para todas las elipses. Una excentricidad de 0 significa que la elipse es un círculo y una elipse larga y delgada tiene una excentricidad que se aproxima a 1.