Contenido
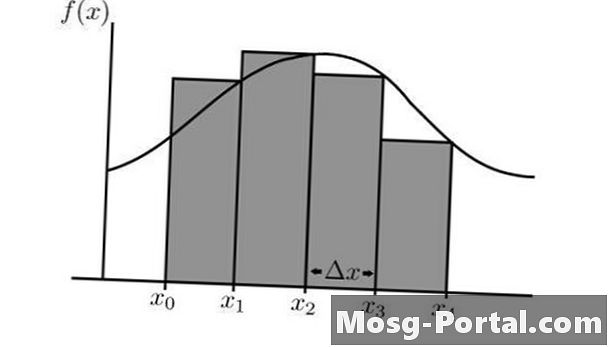
Una suma de Riemann es una aproximación del área bajo una curva matemática entre dos valores X. Esta área se aproxima utilizando una serie de rectángulos que tienen un ancho de delta X, que se elige, y una altura que se deriva de la función en cuestión, f (X). Cuanto menor sea el delta X, más precisa será la aproximación. La altura se puede tomar del valor de la f (X) a la derecha, el centro o la izquierda del rectángulo. Puede aprender a calcular una suma de Riemann a la izquierda.
Encuentre el valor de f (X) en el primer valor de X. Como ejemplo, tome la función f (X) = X ^ 2, y estamos aproximando el área bajo la curva entre 1 y 3 con un delta X de 1; 1 es el primer valor de X en este caso, entonces f (1) = 1 ^ 2 = 1.
Multiplique la altura, como se encuentra en el paso anterior, por delta X. Esto le dará el área del primer rectángulo. Para el ejemplo, 1 x 1 = 1.
Agregue delta X al primer valor X. Esto le dará el valor X en el lado izquierdo del segundo rectángulo. Para el ejemplo, 1 + 1 = 2.
Repita los pasos anteriores para el segundo rectángulo. Continuando con el ejemplo, f (2) = 2 ^ 2 = 4; 4 x 1 = 4. Esta es el área del segundo rectángulo en el ejemplo. Continúe de esta manera hasta que haya alcanzado el valor X final. Para el ejemplo, solo hay dos rectángulos porque 2 +1 = 3, que es el final del rango que se está midiendo.
Agrega el área de todos los rectángulos. Esta es la suma de Riemann. Terminando el ejemplo, 1 + 4 = 5.