Contenido
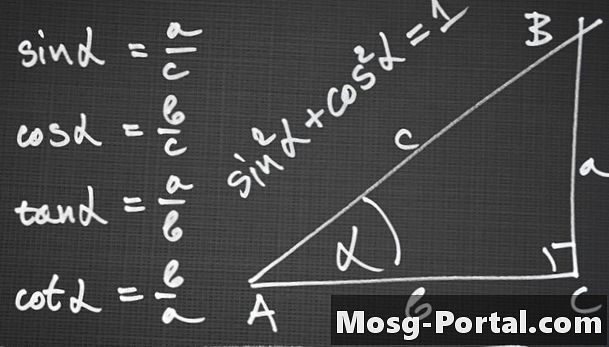
La ley de los senos y la ley de los cosenos son fórmulas trigonométricas que relacionan las medidas de los ángulos de un triángulo con la longitud de sus lados. Se derivan de la propiedad de que los ángulos más grandes en los triángulos tienen lados opuestos proporcionalmente más grandes. Use la ley de los senos o la ley de los cosenos para calcular las longitudes de los lados de un triángulo y un cuadrilátero (un cuadrilátero es esencialmente dos triángulos adyacentes) si conoce la medida de un lado, un ángulo y un lado o ángulo adicional.
Calcular longitudes laterales de triángulo
Encuentra los datos del triángulo. Los datos son longitudes de lados y medidas de ángulos que ya se conocen.No puede encontrar la medida de las longitudes de los lados de un triángulo a menos que conozca la medida de un ángulo, un lado y otro lado u otro ángulo.
Use los datos para determinar si el triángulo es un triángulo ASA, AAS, SAS o ASS. Un triángulo ASA tiene dos ángulos como datos, así como el lado que conecta los dos ángulos. Un triángulo AAS tiene dos ángulos y un lado diferente como da. Un triángulo SAS tiene dos lados como datos, así como el ángulo formado por los dos lados. Un triángulo ASS tiene dos lados y un ángulo diferente como los dados.
Usa la ley de los senos para establecer una ecuación que relacione las longitudes de los lados si es un triángulo ASA, AAS o ASS. La ley de los senos establece que las proporciones de los senos de los ángulos de un triángulo y sus lados opuestos son iguales: sin A / a = sin B / b = sin C / c, donde a, byc son las longitudes de los ángulos del lado opuesto A, B y C, respectivamente.
Por ejemplo, si sabe que dos ángulos son de 40 grados y 60 grados y el lado que los une tenía 3 unidades de largo, establecería la ecuación sin 80/3 = sin 40 / b = sin 60 / c (ya conoce el ángulo opuesto el lado que tiene 3 unidades de largo es 80 grados porque la suma de los ángulos de un triángulo es 180 grados).
Usa la ley de los cosenos para establecer una ecuación que relacione las longitudes de los lados si es un triángulo SAS. La ley de los cosenos establece que c ^ 2 = a ^ 2 + b ^ 2 - 2ab_cos C. En otras palabras, el cuadrado de la longitud del lado c es igual a los cuadrados de los otros dos lados menos el producto de esos dos lados y el coseno del ángulo opuesto al lado desconocido. Por ejemplo, si los dos lados fueran 3 unidades y 4 unidades y el ángulo fuera 60 grados, escribirías la ecuación c ^ 2 = 3 ^ 2 + 4 ^ 2 - 3_4 * cos 60.
Resuelve las variables en las ecuaciones para encontrar las longitudes de triángulo desconocidas. Resolver b en la ecuación sen 80/3 = sen 40 / b produce el valor b = 3 sen 40 / sen 80, entonces b es aproximadamente 2. Resolver c en la ecuación sen 80/3 = sen 60 / c produce valor c = 3 sen 60 / sen 80, entonces c es aproximadamente 2.6. De manera similar, resolver para c en la ecuación c ^ 2 = 3 ^ 2 + 4 ^ 2 - 3_4_cos 60 produce el valor c ^ 2 = 25 - 6, o c ^ 2 = 19, entonces c es aproximadamente 4.4.
Calcular longitudes laterales cuadriláteros
Dibuje una diagonal a través del cuadrilátero (elija la diagonal que no incluya ninguna medida de ángulo dada; por ejemplo, si el ángulo A es un dado en el cuadrilátero ABCD, dibuje la diagonal que conecta B y D).
Use los datos para configurar un triángulo ASA, SAS, AAS o ASS. Recuerda que la suma de los ángulos de un cuadrilátero es 360 grados, por lo que puedes encontrar la medida del cuarto ángulo si conoces los otros tres.
Usa la ley de los senos para resolver las longitudes de los lados del cuadrilátero si configuras un triángulo ASA, AAS o ASS. Usa la ley de los cosenos para resolver las longitudes de los lados si configuras un triángulo SAS.