La tangente es una de las tres funciones trigonométricas básicas, las otras dos son seno y coseno. Estas funciones son esenciales para el estudio de los triángulos y relacionan los ángulos del triángulo con sus lados. La definición más simple de la tangente usa las razones de los lados de un triángulo rectángulo, y los métodos modernos expresan esta función como la suma de una serie infinita. Las tangentes se pueden calcular directamente cuando se conocen las longitudes de los lados del triángulo rectángulo y también se pueden derivar de otras funciones trigonométricas.
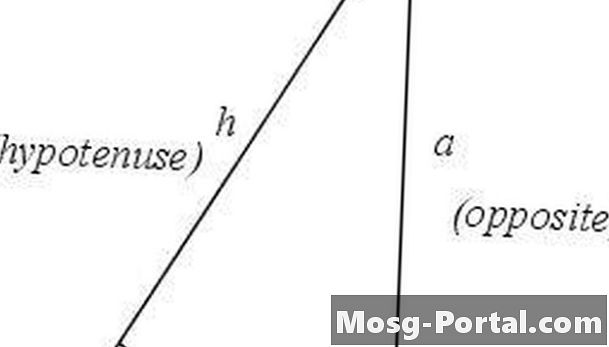
Identificar y etiquetar las partes de un triángulo rectángulo. El ángulo recto estará en el vértice C, y el lado opuesto será la hipotenusa h. El ángulo θ estará en el vértice A, y el vértice restante será B. El lado adyacente al ángulo θ será el lado b y el ángulo opuesto del lado θ será el lado a. Los dos lados de un triángulo que no son la hipotenusa se conocen como las patas del triángulo.
Define la tangente. La tangente de un ángulo se define como la relación entre la longitud del lado opuesto al ángulo y la longitud del lado adyacente al ángulo. En el caso del triángulo en el Paso 1, tan θ = a / b.
Determine la tangente para un triángulo rectángulo simple. Por ejemplo, las patas de un triángulo rectángulo isósceles son iguales, entonces a / b = tan θ = 1. Los ángulos también son iguales, entonces so = 45 grados. Por lo tanto, tan 45 grados = 1.
Derive la tangente de las otras funciones trigonométricas. Como seno θ = a / hy coseno θ = b / h, entonces seno ine / coseno θ = (a / h) / (b / h) = a / b = tan θ. Por lo tanto, tan θ = seno θ / coseno θ.
Calcule la tangente para cualquier ángulo y la precisión deseada:
sen x = x - x ^ 3/3! + x ^ 5/5! - x ^ 7/7! + ... coseno x = 1 - x ^ 2/2! + x ^ 4/4! - x ^ 6/6! + ... Entonces tan x = (x - x ^ 3/3! + X ^ 5/5! - x ^ 7/7! + ...) / (1 - x ^ 2/2! + X ^ 4 / 4! - x ^ 6/6! + ...)