Contenido
- La parábola
- El matemático Menaechmus
- El nombre "Parábola"
- Galileo y movimiento de proyectiles
- Reflectores parabólicos
- Puentes de suspensión
Las curvas matemáticas como la parábola no fueron inventadas. Más bien, han sido descubiertos, analizados y puestos en uso. La parábola tiene una variedad de descripciones matemáticas, tiene una larga e interesante historia en matemáticas y física, y se usa en muchas aplicaciones prácticas en la actualidad.
La parábola
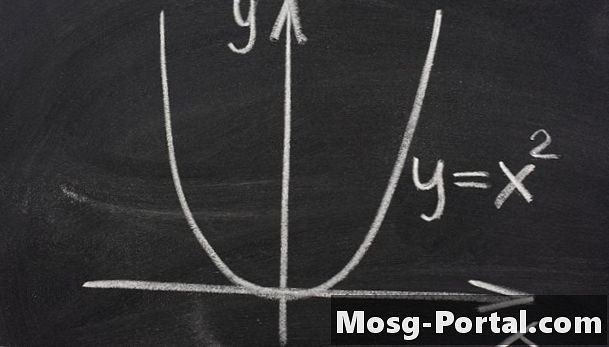
Una parábola es una curva continua que se parece a un cuenco abierto donde los lados siguen subiendo infinitamente. Una definición matemática de una parábola es el conjunto de puntos que están a la misma distancia de un punto fijo llamado foco y una línea llamada directriz. Otra definición es que la parábola es una sección cónica particular. Esto significa que es una curva que ves si cortas un cono. Si cortas en paralelo a un lado del cono, entonces ves una parábola. Una parábola también es la curva definida por la ecuación y = ax ^ 2 + bx + c cuando la curva es simétrica respecto al eje y. También existe una ecuación más general para otras situaciones.
El matemático Menaechmus
Al matemático griego Menaechmus (mediados del siglo IV a. C.) se le atribuye el descubrimiento de que la parábola es una sección cónica. También se le atribuye el uso de parábolas para resolver el problema de encontrar una construcción geométrica para la raíz cubica de dos. Menaechmus no pudo resolver este problema con una construcción, pero sí demostró que puede encontrar la solución intersectando dos curvas parabólicas.
El nombre "Parábola"
Al matemático griego Apolonio de Perga (siglos III al II a. C.) se le atribuye el nombramiento de la parábola. "Parábola" proviene de la palabra griega que significa "aplicación exacta", que, según el Diccionario de Etimología en línea, es "porque se produce por" aplicación "de un área determinada a una línea recta determinada".
Galileo y movimiento de proyectiles
En la época de Galileo, se sabía que los cuerpos caen hacia abajo de acuerdo con la regla de los cuadrados: la distancia recorrida es proporcional al cuadrado del tiempo. Sin embargo, no se conocía la naturaleza matemática de la ruta general del movimiento de proyectiles. Con la llegada de los cañones, esto se estaba convirtiendo en un tema importante. Al reconocer que el movimiento horizontal y el movimiento vertical son independientes, Galileo mostró que los proyectiles siguen un camino parabólico. Su teoría fue finalmente validada como un caso especial de la ley de gravitación de Newton.
Reflectores parabólicos
Un reflector parabólico tiene la capacidad de enfocar o concentrar la energía que viene directamente hacia él. La televisión por satélite, el radar, las torres de telefonía celular y los colectores de sonido utilizan la propiedad de enfoque de los reflectores parabólicos.Enormes radiotelescopios concentran señales débiles desde el espacio para crear imágenes de objetos distantes, y hoy en día se utilizan muchos enormes. Los telescopios reflectores de luz también funcionan según este principio. Desafortunadamente, la historia de que Arquímedes ayudó a un ejército griego a usar espejos parabólicos para prender fuego a las naves invasoras romanas que atacaban su ciudad de Siracusa en 213 a. C. Probablemente no sea más que una leyenda. El proceso de enfoque también funciona a la inversa: la energía emitida hacia el espejo desde el foco se refleja en un haz recto muy uniforme. Las lámparas y transmisores, como el radar y las microondas, emiten haces de energía dirigidos reflejados desde una fuente en el foco.
Puentes de suspensión
Si sostienes los dos extremos de una cuerda, se inclina hacia abajo en una curva, llamada catenaria. Algunas personas confunden esta curva con una parábola, pero en realidad no es una. Curiosamente, si cuelgas pesas de la cuerda, la curva cambia de forma para que los puntos de suspensión se encuentren en una parábola, no en una catenaria. Entonces, los cables colgantes de los puentes colgantes en realidad forman parábolas, no catenarias.