Un triángulo equilátero es un triángulo con los tres lados de igual longitud. El área de superficie de un polígono bidimensional, como un triángulo, es el área total contenida por los lados del polígono. Los tres ángulos de un triángulo equilátero también son de igual medida en geometría euclidiana. Dado que la medida total de los ángulos de un triángulo euclidiano es de 180 grados, esto significa que todos los ángulos de un triángulo equilátero miden 60 grados. El área de un triángulo equilátero se puede calcular cuando se conoce la longitud de uno de sus lados.

Determine el área de un triángulo cuando se conocen la base y la altura. Tome dos triángulos idénticos con base s y altura h. Siempre podemos formar un paralelogramo de base s y altura h con estos dos triángulos. Como el área de un paralelogramo es s x h, el área A de un triángulo es, por lo tanto, ½ s x h.

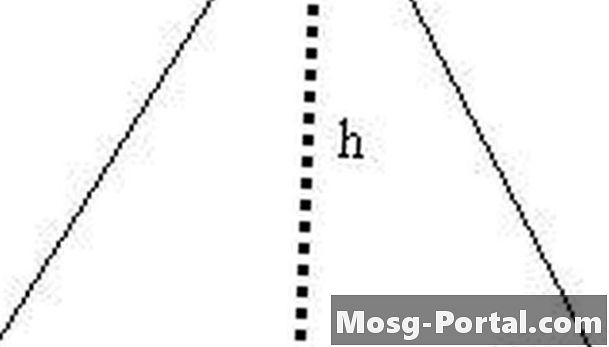
Forma el triángulo equilátero en dos triángulos rectángulos con el segmento de línea h. La hipotenusa de uno de estos triángulos rectángulos longitud s, una de las patas tiene longitud h y la otra pierna tiene longitud s / 2.
Exprese h en términos de s. Usando el triángulo rectángulo formado en el paso 2, sabemos que s ^ 2 = (s / 2) ^ 2 + h ^ 2 por la fórmula pitagórica. Por lo tanto, h ^ 2 = s ^ 2 - (s / 2) ^ 2 = s ^ 2 - s ^ 2/4 = 3s ^ 2/4, y ahora tenemos h = (3 ^ 1/2) s / 2.
Sustituya el valor de h obtenido en el paso 3 en la fórmula para un área de triángulos obtenida en el paso 1. Como A = ½ sxh y h = (3 ^ 1/2) s / 2, ahora tenemos A = ½ s (3 ^ 1/2) s / 2 = (3 ^ 1/2) (s ^ 2) / 4.
Usa la fórmula para el área de un triángulo equilátero obtenido en el paso 4 para encontrar el área de un triángulo equilátero con lados de longitud 2. A = (3 ^ 1/2) (s ^ 2) / 4 = (3 ^ 1/2 ) (2 ^ 2) / 4 = (3 ^ 1/2).